結び目の数理セミナー Knotting Nagoya 会合案内
メインへ
- 日時:11月8日(土)13:00 ~
- 場所 : 名古屋工業大学 53号館 3階建部分の3階 5234教室
- 講演者:山本 亮介(大谷大学)、斎藤敏夫(上越教育大学)
- 題目:COMPLEXITY OF OPEN BOOK DECOMPOSITIONS VIA ARC COMPLEX
- アブストラクト:
- Heegaard 分解の Hempel 距離の類似物を有向閉3次元多様体の open book 分解において定義し、 その値と open book 分解のファイバー曲面の幾何的構造との関係を解説する。 まずは、open book 分解の基本変形とファイバー曲面上の proper arc の monodromy による動きとの関わりを整理したあと、 open book 分解の "translation distance" をファイバー曲面の arc complex 上の距離として導入し、主結果とその証明を紹介する。
・名工大 会場案内 (名古屋 新幹線ホームより30分程度)
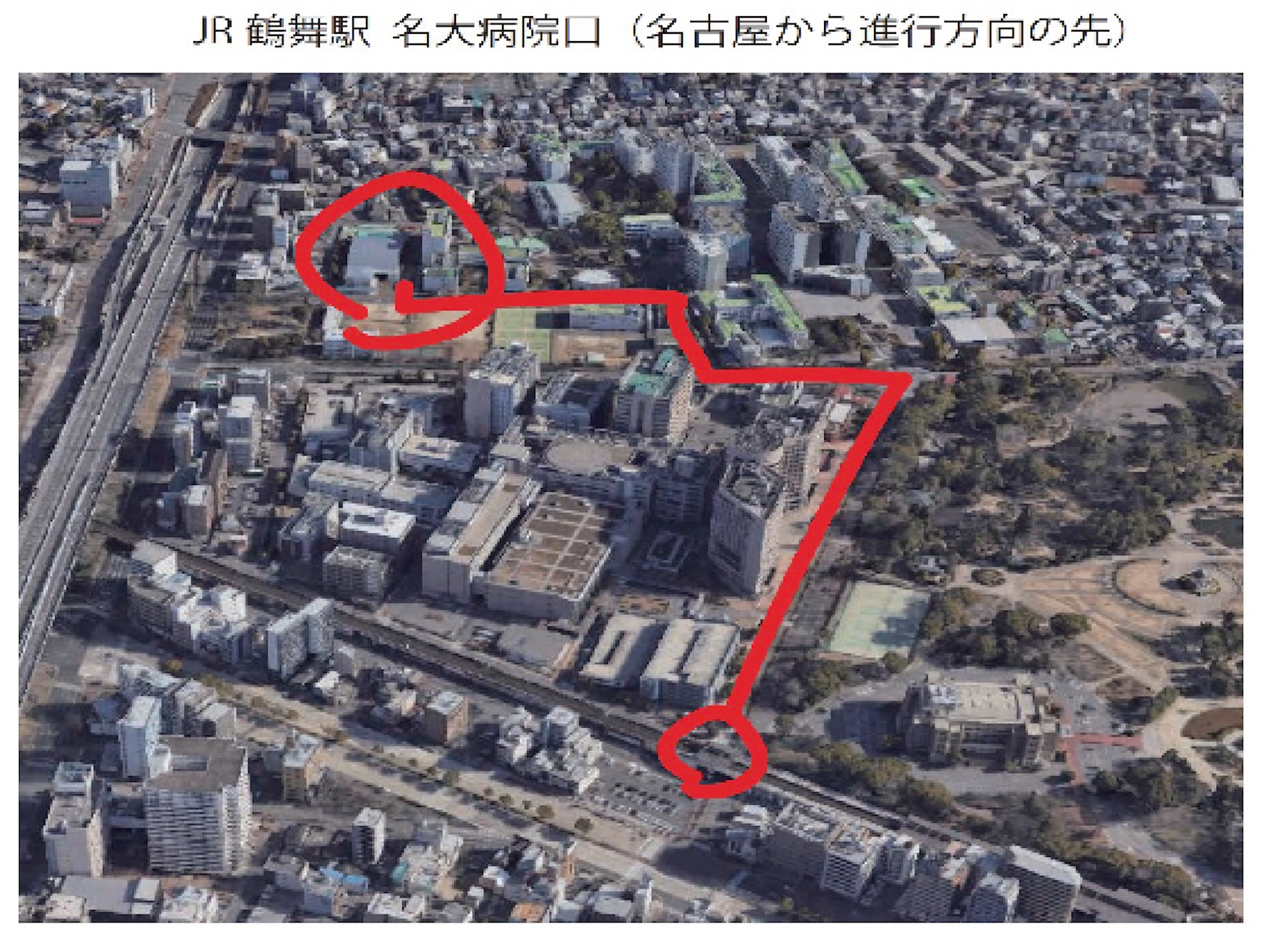
JR中央本線にて,名古屋から2駅目 鶴舞駅 (金山の次)より
進行方向側の出口(名大行院口)より徒歩.
体育館向かいの3階建の3階の5234教室、(入って左手にエレベータあり)

- 「Knotting Nagoya and Nagoya City University Seminar (No. 176) 」
Date:July 14th(Mon)15:00 ~ 16 - Place : Nagoya City University
- Nagoya City University Takiko campus, Building No.4, 3rd floor Main Lecture Room
-
467-8501 名古屋市 瑞穂区 瑞穂町 山の畑1 名古屋市立大学
access
map - Speaker: Sam Nelson (Claremont McKenna College)
- Title: Quiver Categorification of Homset Invariants
- Abstract:
-
The quandle coloring quiver and similar constructions provide a way of turning homset- based invariants into categories.
In this talk we will examine this phenomenon with several examples.
2024年度会合
2020-2023
2019年度会合
2018年度会合
2017年度会合
2015年度会合
2014年度会合
2013年度会合
2012年度会合
2011年度会合
2010年度会合
2009年度会合
リンク
OCAMI:大阪公立大学 数学研究所
新KOOKセミナー事務局